TL;DR -- Following up on our theme, we look at a recent bit of controversy from a deeper than normal position. Computers are nice to have for many reasons. They can be problematic. Just like technology being great when it works, so too are computers. Given problems, then results can range widely. With numbers (say, your bank balance), we have come to expect accuracy. What if the computer system could not provide this? Ought it be released?
---
We have noted that technology has been a huge influence on our lives, for the most part good. But, that is questionable if one looks at all of the side-effects of change with consideration for ramifications. Like, why are whales washing up on shore now? It's too early to tell, but we can go through the whole litany of issues seen. Ought to, perhaps, with the expectation that computing's list would be long.
Especially is this so if we start with the internet's start which we could put at 30 years ago, about, if we assume the release of the protocol and its being handed to the public. We can look at more than the 'wild west' emergence in the cyber real, and its accompanying, real space, for one thing. But, there are many things to look at.
Engineering works to improve which we have seen with hardware. Again, though, reuse is nil which can be seen with the piles of computer junk everywhere. Software, even, grew more mature using other types of engineering practices.
Machine learning has been in the news of late which hoped to demonstrate that the computer could learn on its own. This post is about one example of that which has been much in the press, lately:
ChatGPT. There are others that are now ready to go (with respect to the opinion of the team doing the work) or coming up quickly.
OpenAI pushed out ChatGPT, perhaps premturely, in November. We didn't pay attention until last month. The news reports have many articles about misuse or downright errorful ways of the thing. The USA Today had a headline this week that Microsoft was putting ChatGPT in its Bing product (rival of Google's Chrome and replacement of its Internet Explorer) but is doing so without any guarantee of accuracy (see below). Marketing types are touting that they are using the thing for the creation of ad material. Students are trying to use it for essay assignments. Some are trying to do software using it.
Then, we have the associated work related to fake photos and videos being created, many times without any warning with respect to the reader about provenance. Does truth in advertising mean anything? The below is about fake math which is easier to see, as text is much harder given the power of language.
Now, this example came from noting that a younger person wrote that they were making progress learning Calculus 3 via ChatGPT. Oh? After a few queries to clarify the matter and making a few suggestions to stay safe, we went to look at this part of ChatGPT. We have already seen the code generation aspect and were going to try it out, in an experimental manner, as since John had done something similar a couple of decades ago.
Well, where to start. Calc 3 is too advanced for a beginning look, so we dropped down to Calc 1 & 2 which would be fundamental. We asked for the 'integral of sin theta' which was phrased this way due to the conversational mode that is being emphasized as a benefit. Well, math is terse for the reason that it is difficult to write something similar to a complicated question in a natural language. Too, we have decades now of work on computational mathematics which was to be somewhat the ground truth in this matter since it is a creation of humans with lots of time involved in making it right.
But, on taking in the query, the thing (CP for ChatGPT) did not just say that it was '-cos theta' but added in some verbiage about the indefinite status of this result and why it had to add in a constant. That's fine. Tables of integrals have been published almost from the beginning. Some are quite extensive. Too, some of the rules are known.
 |
ChatGPT
and a trig example |
Now, one huge question is whether the rules are explicit enough to invoke proper action. The analog here? Code. It is explicit, given the framework. Some code is more involved than others. But, all of them shuffle down to something that the hardware can use to do its thing.
And, machine learning (ML) using books would have seen these tables and rules. Now, what we need to look at is what the ML did with what it saw which involves transforms and iterations and some clever tweaking. The guidance, supposedly, for this work is the human brain. We cannot fall into that argument's pit; the equivalence is not there, except in a very limited way.
What would be the next step? Mind you, we had not thought to refer, yet, to the experts and their systems that one can see on the computer. We went looking for something gnarly but not too much so. As, we would have to verify the result given by CP. We saw this example, as it was being explained on youtube.
Namely, the function that was taken to use: arcsin(x) * arccos(x) * 1/x. The query would be to get the integral of this. Now, text input, right? And, not thinking of converting to some code'ish mode, we put the query in using a verbose mode. Again, there was no thought taken for the limiting constraints that would be part of an actual calculation.
The query was something like this (the actual logs were saved). What is the integral of the arcsin of theta times the arccos of theta divided by theta? CP repeated the input in a more formulaic mode. This was to confirm having parsed the query correctly. Then, CP started to explain that it would do integration by parts and started down its path which turned out to be fairly long. That was unexpected.
Why? We are talking an approach where a model gets developed from the processing of the data. Then, a query would consist of extracting (via clever means) an answer.
Now, as an aside, what got everyone excited about these things is that they won games. And, in some cases, they learned the game by looking at the rules. Or, more of note, by studying data related to a game, discovered the rules and even beat human experts. Winning the Go game is an example of the shock value of this approach. Only the brainy were good at these games.
Also, this technique is not new. What is new is better systems plus less emphasis on the cultural norms of systems development which can be explained. In the lax environment, the thing could venture in spaces where humans never went, thereby finding out things that humans would not have seen.
Well, actually, that is a benefit of computing that we need to exploit. Take chemistry. The computer allows modeling of lab experiments in numbers not possible in reality where time, costs, resources, and a whole lot more bear on, constrain, the situation. Too, we have to take on some faith that the computer simulation has meaning. We, as a whole, lack experience in that area since it is so new. And, this is to be discussed further.
So, CP pushing out its steps (almost trace) was bothersome. For one thing, reading and checking these type of things consumes time and energy. It can be done. Engineering students are used to this. In the past, hand calculation was more the way of learning than now. As we considered the potential for a growing pile of computed stuff to prove, our thoughts went to Sisyphus and his lesson for us.
The computer can spit out a new universe. What's to believe about it? And, then, how do we prove something? Oh, that's the crux of the matter. We will discuss truth engineering as one factor, but this is a hard problem that will get worse.
So, we did two things. We went to Wolfram and did the integration. However, something reminded us of the huge lack. Gaming and all of those non-real computing experiences might have numbers, but they really have no meaning. On the other hand, real-world requirements demand proper use of numbers with respect to measure. Whole theories and practices deal with this topic.
Too, we humans use numbers quite extensively and readily. But, some means are better, say algebraic analysis, than others. Again, this is a known area of research and practice. So, the notion was to move away from the indefinite mode and get definite. That means to put limits on the integration which relates, in this case, to determining an area. The interplay of geometry and algebra is core to calculus (and its companion of old - seemingly lost - of analytic geometry).
Wolfram calculated the area. Well, we went and found another on-line calculator. BTW, these tools follow known mathematical principles and can be tested. In fact, software engineering is a common mode of program management for this type of system. Something that does not perform correctly will be noted. And, corrected.
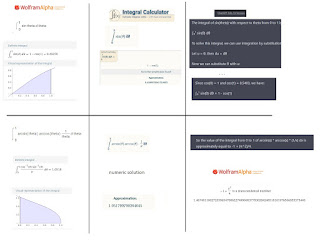
Now, the graphic shows the 'sin' integration by the three parties: Wolfram; Integral Calculator; and CP. They all agreed with the number for the area which is reported on the first row. The second row has the results of the more gnarly function which actually is quite simple. It behavior at the limits is what makes it interesting.
Now, for the second case (row), Wolfram did a symbolic calculation. This is the equational manipulation method which produces exact results if done correctly. These two examples use trig functions that are well known. BTW, there is a book from the government that give standard mathematical usages, values and more for use by those who need to used mathematics. In one of these, the derivatives (which are the results of integration - in a sense) are given in only a few pages. Going the other way, from the derivative to the integral has many more pages due to the complexity. And, trig functions account for lots of these pages.
The answer by Integral Calculator agreed with Wolfram. But, with a twist. That attempt bailed out of the closed form solution (so, kudos to Wolfram for following through) and did a numeric solution. Now, those are the two major themes for math solutions. Proof theoretic modes are being ignored, for now. One can algebraically solve something. The answer will be exact. Or, one approximates through techniques that grew up with the computer. These methods are harder as they have to be highly detailed through the process.
We used an example, formerly (four decades ago?), that dealt with a guy spending 10 years solving a system of equations. This would have been a mixture of symbolic and numeric. Then, he spent 10 years verifying the work. Then, a computer could do that work in a few minutes. Now? It would be a less than batting an eye. Of course, speed of error goes around as fast as does the right solution. We have to learn to handle technology with regard to these types of issues.
So, simple table lookup? Not really. Even with the 'sin' problem, CP went through its model which was built using gobs and gobs of computer time and energy and data. The marketing view says that CP was trained on the internet which would include pages of people, things like Wikipedia (which is good) and books. As well, if we proceeded with integrals, there are many times when one has to transform some equation (or series of equations) to something equivalent. That is, the movement would be from something not in the table, to something that is. If that works, then it's fine, except it can be a fairly gnarly equation and one has to remember how to reverse back to the former look. Much to discuss there.
Now, CP? For the gnarly example, it went the 'by parts' route and detailed its work. But, it was not doing a step by step in the sense that we might think. We have to look deeper. In any case, it gave an answer that did not agree with Wolfram or the Integral Calculator. Oh, CP was right? They are wrong? It doesn't work that way in math.
A little bit of additional information? CP gave different answers based upon sleight changes in input. We showed that by nudging it to remember that it knew Thomas Gardner (see prior post). In fact, nudging is a known and acceptable approach. Even though, this might lead one to think about fudging.
There is a difference. Nudging works by changing parameters (inputs) in order to guide the problem solver. It takes into account various mathematical notions that have a history and support. Fudging, on the other hand, is after the fact. But, again. This same type of thing could be said about fuzzy approaches (which are quite powerful) or even any type of 'post' processor which takes output and makes it suitable for the eyes of managers. Too, though, there is a thing called integer programming which, briefly, gets to some area and then refines to a solution.
Our interest is bridging the world of ourselves, typical humans, with that of experts who have to deal with specifics of domains plus all of the realities that pertain to using computers.
Remarks: Modified: 08/26/2023